Nace de la necesidad del hombre , estos nacieron en la India.
El mas antiguo es el sistema d numeración es el Hindú y se transmitió a Europa por los árabes , fibonacci fue testigo de la transmisión de este sistema y fue el que vio la necesidad de incorporar el (0).
LOS NÚMEROS REALES COMO UN CAMPO
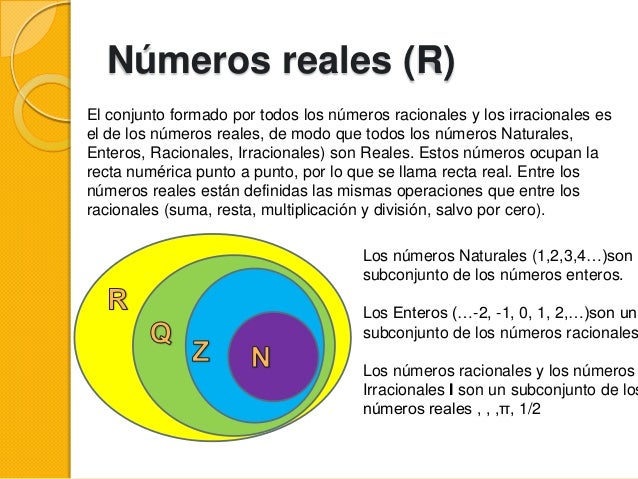

Todo aquel conjunto de números racionales e irracionales.
Racionales: Participan los decimales y los quebrados
Irracionales: Números que tienen cantidad infinita de decimales que no de repitan
Axiomas de números reales
-Divisores y múltiples de un entero
Si A como y C pertenecen a los enteros cumple la relacion C=A*B entonces decimos que
A y B son factores o divisores de C en tal caso C es multiplo de A y B.
C= a.b
C: es el multiplo
a.b:es el que divide el multiplo
Ej:
20=5.4
30=6.5
-Un numero entero es divisible por 2:
si termina en 0 o en cifra par
-un numero entero es divisible por 3:
si la suma de sus cifras es múltiplo 3
-un numero es divisible por 4:
si sus dos ultimas cifras son 0 0 o son múltiplo de 4
-un numero es divisible por 5:
si termina en 0 o en 5
-un numero es divisible por 6:
si lo es divisible por 2 y por 3 a la vez
-no hay regla para 7
-un numero es divisible para 8.
si sus 3 ultimas cifras es 0 0 0 o es multiplo de 8
-un numero es divisible para 9:
si la suma de sus cifras es multiplo de 9
-un numero es divisible para 10:
si termina en 0
Teoremas de numeros reales
Todo numero compuesto se puede descomponer de manera unica como el producto de numeros primos.
-Teorema fundamental del máximo común divisor
Que un conjunto de numeros enteros es el mayor entero positivo que es divisor de cada uno de los numeros del conjunto.
Ejemplo:
-Teorema fundamental del mínimo común múltiplo
El M.C.M de un conjunto de números enteros es el menor entero positivo que es el múltiplo de cada numero dado.para poderlo sacar tenemos excojer los comunes con el mayor de los exponentes y los que no se repiten.
1.un fabricante tiene 3 productos en su inventario , los cuales se revisa periódicamente cada 2,6 y 10 semanas respectivamente.El fabricante necesita calcular cual sera el mínimo tiempo que debe transcurrir en semanas para que la revisión de los 3 productos coincidan.
x
2. Una cita en Sevilla
un viajante va a Sevilla cada 18 días , otro va a Sevilla cada 15 días y un tercero va a Sevilla cada 8 días. hoy día 10 de junio a concebido los 3 días antes .dentro de cuantos días como mínimo volverá a concebir en Sevilla.
M.C.M=23X32X5=360
NÚMEROS PARES E IMPARES
PARES:Los números pares, son en matemáticas aquellos números enteros múltiplos del número 2. Por el hecho de ser enteros incluye tanto a números positivos como negativos. Todos aquellos que no sean múltiplos de dos les llamaremos números impares. Esta es una clasificación excluyente, es decir, los números serán o pares o impares, pero nunca podrán ser a la vez pares e impares. Además, obligatoriamente deben pertenecer a uno de los dos conjuntos.
Las operaciones entre pares, siempre dan como resultado un numero par. Veamos algunos ejemplos para demostrar esta afirmación:
- Suma: 2+4=6, 4+8 = 12.
- Resta: 6-4=2, 10-2=8.
- Multiplicación: 4×4 = 16, 10 x 2 = 20.
- División: 8/4 = 2, 16/2 = 8.
IMPARES:Los números impares, son en matemáticas aquellos números enteros que no son múltiplos del número 2 a diferencia de los pares que son múltiplos de dos.
Algunas de las operaciones entre números impares, dan como resultado un numero par otras resultan en un impar. Con algunos ejemplos apreciaremos este hecho
- Multiplicación: 3×3 = 9 (I)
- División: 9/3=3 (I)
JERARQUÍA DE OPERACIONES

EJEMPLO:
REPRESENTACIÓN DECIMAL
Existen diferentes tipos de decimales como son:
Decimal finito
periódica infinito
periódica mixto
infinito no periódica

RAZONES Y PROPORCIONES
Razón
Razón o relación de dos cantidades es el resultado de comparar dos cantidades.
Dos cantidades pueden compararse de dos maneras: Hallando en cuánto excede un a la otra, es decir, restándolas, o hallando cuántas veces contiene una a la otra, es decir, dividiéndolas. De aquí que haya dos clases de razones: razón aritmética o por diferencia y razón geométrica o por cociente.
Razón aritmética o por diferencia de dos cantidades es la diferencia indicada de dichas cantidades.
Las razones aritméticas se pueden escribir de dos modos: Separándolas dos cantidades con el signo ― o con un punto (.). Así, la razón aritmética de 6 a 4 se escribe:
6―4 ó 6.4 y se lee seis es a cuatro.
Los términos de la razón se llaman: antecedente el primero y consecuente el segundo. Así, en la razón 6―4, el antecedente es 6 y el consecuente 4.
Razón geométrica o por cociente de dos cantidades es el cociente indicado de dichas cantidades.
Las razones geométricas se pueden escribir de dos modos: En forma de quebrado, separados numerador y denominador por una raya horizontal o separadas las cantidades por el signo de división (¸). Así, la razón geométrica de 8 a 4 se escribe u 8¸4 y se lee ocho es a cuatro.
u 8¸4 y se lee ocho es a cuatro.
Los términos de la razón se llaman: antecedente el primero y consecuente el segundo. Así, en la razón 8¸4, el antecedente es 8 y el consecuente 4.
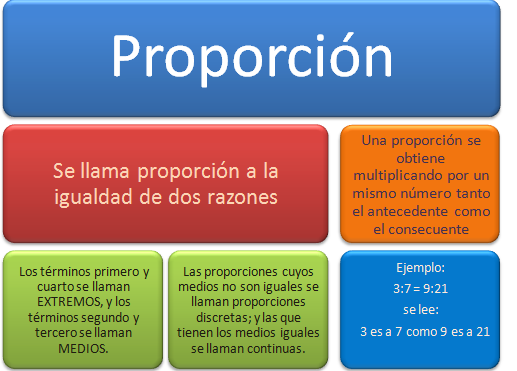
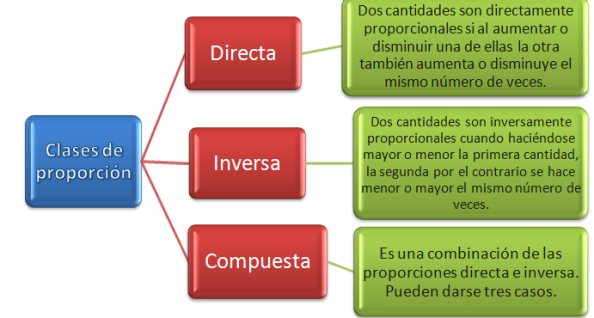
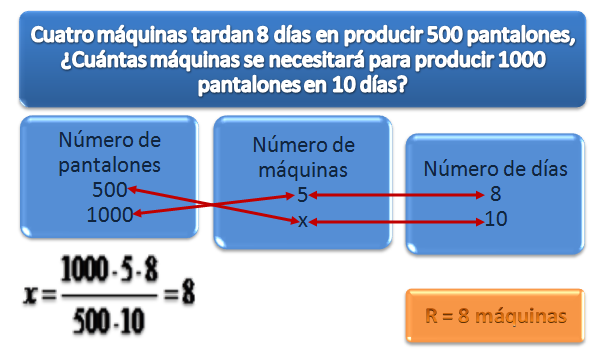
EJEMPLOS
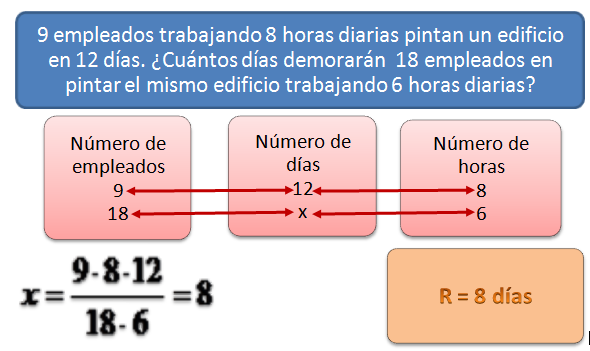
INTERVALOS
Se trata de una determinada distancia.
es el conjunto de todos los numero de a.b donde a.b son los extremos entonces se podría decir que el intervalo es la distancia.
Tipos de Intervalo
Intervalos abiertos: (a,b): Son todos los números entre a y b sin incluir sus extremos.
Intervalos cerrados: [a,b]: Son todos los números entre a y b incluyendo sus extremos.
Intervalos semiabiertos o semicerrados: [a,b) Son todos los números entre a y b incluyendo el extremo a.
Intervalos infinitos: (a,∞) : Son todos los números mayores que a.
Ejemplos:
a) El intervalo [-2, 3] comprende todos los números reales entre -2 y 3. Como es cerrado incluye los extremos. Su representación gráfica es:
b) El intervalo (1, 4) corresponde a todos los números reales entre 1 y 4. Es abierto pues no incluye a los extremos. Gráficamente:
c) El intervalo (0, 5] comprende todos los números reales entre 0 y 5 incluyendo el extremo 5. Se trata de un intervalo semiabierto a izquierda o bien semicerrado a derecha. Su gráfica es:
d) El intervalo [1, +¥ ) es infinito y comprende todos los números reales mayores o iguales a 1. Gráficamente:
e) El intervalo (-¥, 3) es infinito y comprende todos los números reales menores que 3. Su gráfica es:
ECUACIONES
Una ecuación o igualdad condicional es aquella que es verdadera solo para algún o algunos valores de la variable del conjunto referencial que corresponda.
Propiedades de las ecuaciones
1:∀x,y є ℝ,(x=y)=(y=x)
2:∀x,y є ℝ,∧ c є ℝ,(x=y)=(x+c=y+c)
3:∀x,y є ℝ,∧ c є ℝ,(x=y)=(x.c=y.c)
4:∀x,y є ℝ-{0}, (x=y)=(xn=yn),n є ℤ
5:∀x,y є ℝ,(X.Y=0)=(X=0 ∨ Y=0)
Ecuaciones lineales
Las ecuaciones lineales de primer grado son del tipo ax + b = 0 , con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adopten esa expresión.
Ejemplos
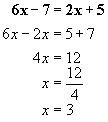
Ecuaciones Cuadráticas
Una ecuación cuadrática o de segundo grado es aquella que se puede representar con un predicado de la forma ax2 + bx + c, donde a, b, y c son números reales.
Existe una fórmula que permite resolver cualquier ecuación de segundo grado, que es la siguiente:

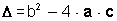
Una ecuación cuadrática o de segundo grado es aquella que se puede representar con un predicado de la forma ax2 + bx + c, donde a, b, y c son números reales.
Ejemplo:
x2 + 5x - 10 (x+6)(x-1)
x+6=0 x-1=0
comprobación
x2 + 5x - 10
(-6)2+5(-6)-6=0
36-30-6=0
36-36=0
0=0
x2 + 5x - 10
(1)2+5(1)-6=0
1+5-6=0
6-6=0
0=0
Solución por la forma general
Existe una fórmula que permite resolver cualquier ecuación de segundo grado, que es la siguiente:
La fórmula genera dos respuestas: Una con el signo más (+) y otra con el signo menos (−) antes de la raíz. Solucionar una ecuación de segundo grado se limita, entonces, a identificar las letras a, b y c y sustituir sus valores en la fórmula.
La fórmula general para resolver una ecuación de segundo grado sirve para resolver cualquier ecuación de segundo grado, sea completa o incompleta, y obtener buenos resultados tiene que ver con las técnicas de factorización.
pero existe El radicando b2 – 4ac se denomina discriminante y se simboliza por Δ. El número de soluciones (llamadas también raíces)depende del signo de Δ y se puede determinar incluso antes de resolver la ecuación.
Reglas del discriminante
Si el Δ es mayor que el cero existen dos soluciones.real y diferente
Si el Δ es igual a cero , hay una solución real duplicada
Si Δ es menor que cero, no existe solución real .
Ejemplo de la formula general.

VALOR ABSOLUTO
Valor absoluto de un número real a, se escribe |a|, es el mismo número a cuando es positivo o cero, y opuesto de a, si a es negativo.
Ejemplo:El valor absoluto lo escribiremos entre barras verticales.
|−5| = 5
|5| = 5
Propiedades
-Los números opuestos tienen igual valor absoluto
-El valor absoluto de un producto es igual al producto de los valores absoluto de sus factores
-El valor absoluto de una suma es menor o igual a la suma de los valores absolutos o de los sumando.
INECUACIONES
Es una desigualdad algebraica .
Ejemplos:
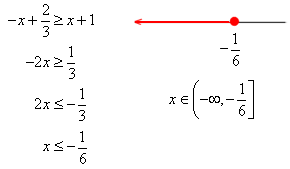



 Q)=150 N[Re-(
Q)=150 N[Re-(

